Spherical Cone vs Sphere Intersection Test

I’m sharing here a different flavour of the cone vs. sphere intersection test that we used to improve the culling of spotlights in our Lightmapper.

To accelerate lighting evaluation, our Lightmapper uses a grid structure that subdivides the scene into cubic cells. For each cell we compute the list of lights whose bounding volume overlaps the cell’s bounding box. As no trivial AABB vs. cone exists, a common strategy is to compute instead the intersection test between the cone and the cell’s bounding sphere. You can find the code for that approach on Bart Wronki’s blog.

For a spotlight it’s actually possible to compute a tighter bound than a cone, considering that spotlights are usually implemented in rendering engines as point lights with an angular falloff. Effectively, the bounding shape for a spotlight is not a cone but what’s called a spherical sector (also called spherical cone). That tighter bound formulation is particularly interesting if your spotlight has a wide angle.

And it turns out it’s not too complicated to craft an intersection test between a spherical sector and a sphere. The gist of the idea is to compute the portion of the sphere that intersects with the sphere supporting the cone. You end up with the description of a second spherical sector:

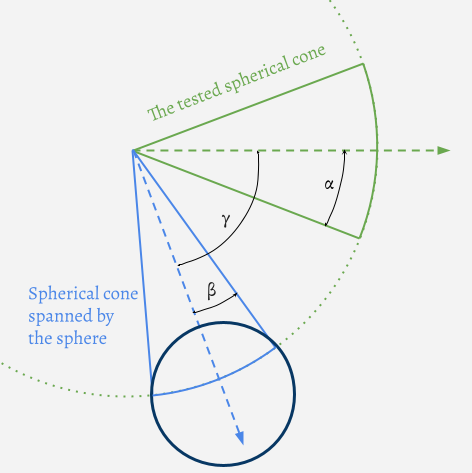
It’s then just a matter of finding out if the 2 spherical sectors intersect. Given the half angles α and β of the 2 spherical sectors and the angle γ between their 2 axes, the spherical sectors intersect if: α + β > γ

To compute the second spherical sector we need 2 distinct formulas, depending on how far the sphere is from the cone’s origin. Let’s go through them, the notations used are summarized in the following table.

Cr	Cone radius
Sr	Sphere radius
d	Distance from the cone origin to the sphere center
alpha (α)	Half-angle of the cone
beta (β)	Half-angle of the spherical sector spanned by the sphere
gamma (γ)	Angle between the 2 sector’s axes

• Formula A: The tested sphere is mostly inside the cone’s supporting sphere

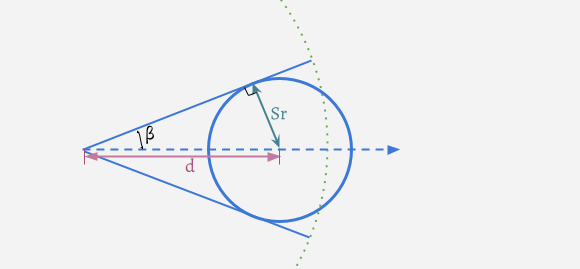Then, the second spherical sector is tangent to the sphere and its angle is given by: sin(β) = Sr / d

• Formula B: The tested sphere is mostly outside the cone’s supporting sphere

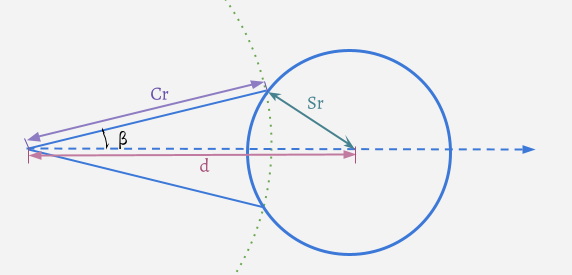Then, from the law of cosines: cos(β) = (d² - Sr² + Cr²) / (2*Cr*d)

When the Cr, Sr and d segments form a right triangle, we are sitting inbetween these 2 cases. That can be used to determine which formula we should use to compute the spherical sector. If d² < Sr² + Cr², then Formula A is used; otherwise, Formula B is used.

Putting everything together, here is a first naive implementation of our IntersectSphericalConeWithSphere test in HLSL:

bool IntersectSphericalConeWithSphere(
    float3 coneOrigin, float3 coneForward, float coneRange, float coneHalfAngle,
    float3 sphereOrigin, float sphereRadius)
{
    const float Cr = coneRange;
    const float Sr = sphereRadius;
    const float Cr2 = Cr * Cr;
    const float Sr2 = Sr * Sr;
    const float3 V = sphereOrigin - coneOrigin;
    const float d2 = dot(V, V);
    const float d = sqrt(d);

    // Sphere outside of cone's bounding sphere
    if (d2 >= (Cr + Sr) * (Cr + Sr))
        return false;

    // Cone center is inside the sphere
    if (d2 < Sr2)
        return true;

    const float alpha = coneHalfAngle;
    const float beta = (d2 < Sr2 + Cr2) ? asin(Sr / d) : acos((d2 - Sr2 + Cr2) / (2*Cr*d));
    const float gamma = acos(dot(V, coneForward));

    // The spherical sectors intersect if: (α + β) > γ
    return (alpha + beta) > gamma;
}

asin and acos are quite expensive to evaluate on the GPU (For a deeper look into their performance impact, see this article or this one). We can avoid them by massaging a bit the condition:

α + β > γ

=> cos(α + β) < cos(γ) (the comparison is inverted because the cosine function is decreasing on (0,π))

=> cos(α)cos(β) - sin(α)sin(β) < cos(γ)

=> cos(α)cos(β)*d - sin(α)sin(β)*d < cos(γ)*d

The optimized test then becomes:

bool IntersectSphericalConeWithSphere(
    float3 coneOrigin, float3 coneForward, float coneRange, float coneHalfAngle,
    float3 sphereOrigin, float sphereRadius)
{
    const float Cr = coneRange;
    const float Sr = sphereRadius;
    const float Cr2 = Cr * Cr;
    const float Sr2 = Sr * Sr;
    const float3 V = sphereOrigin - coneOrigin;
    const float d2 = dot(V, V);

    // Sphere outside of cone's bounding sphere
    if (d2 >= (Cr + Sr) * (Cr + Sr))
        return false;

    // Cone center is inside the sphere
    if (d2 < Sr2)
        return true;

    // Compute the half angle β of the spherical sector that is spanned by the sphere  
    const bool sphereIsClose = (d2 < Sr2 + Cr2);
    const float a = sphereIsClose ? Sr : (d2 - Sr2 + Cr2) * 0.5f * rcp(Cr);
    const float b = sqrt(d2 - a * a);
    const float cosBetaMultD = sphereIsClose ? b : a;
    const float sinBetaMultD = sphereIsClose ? a : b;

    // Angle γ is between the sphere direction and the cone direction
    const float cosGammaMultD = dot(V, coneForward);

    // cos and sin of the cone half angle, precompute if possible
    const float cosAlpha = cos(coneHalfAngle);
    const float sinAlpha = sin(coneHalfAngle);

    // The spherical sectors intersect if: (α + β) > γ
    return (cosAlpha * cosBetaMultD - sinAlpha * sinBetaMultD) < cosGammaMultD;
}